UABDivulga - Barcelona recerca i innovació

El moviment Brownià fraccional (fBm) és una generalització del més ben conegut procés de moviment Brownià, i va ser originàriament introduït per Kolmogorov l'any 1940 en relació amb el modelatge de turbulències, encara que el seu nom prové de l'influent article de Mandelbrot i Van Ness (1968). El fBm és un procés estocàstic depenent d'un paràmetre H (a (0,1)), anomenat "índex de Hurst" per l'hidròleg anglès que va estudiar els registres dels màxims del riu Nil en relació amb el disseny de pantans l'any 1951. El procés de moviment Brownià estàndard correspon al cas H=1/2. Aquest procés és auto-similar (o invariant per canvi d'escala) i en el cas H>1/2 els increments mostren dependència a llarg termini. Aquestes dues propietats fan que el fBm jugui un paper molt important en modelització.

Per exemple, en el tràfic sobre xarxes es pot observar la presència de dependència a llarg termini (anomenada Efecte Josep) així com la de patrons d'auto-similitud. Una explicació física senzilla per a això és la superposició de moltes fonts On/Off de fluid per a la xarxa amb períodes On/Off estrictament alterns i tals que les longituds dels períodes On/Off tinguin gran variabilitat (o "cues pesades", d'això se'n diu Efecte Noé): Taqqu, Willinger i Sherman van provar l'any 1997 que la superposició de moltes d'aquestes fonts genera un procés d'arribades acumulat (fins a cada instant de temps) agregat que canviat d'escala convenientment convergeix en cert sentit a un fBm, i relacionen el paràmetre que descriu la intensitat de l'Efecte Noé dels períodes On/Off amb l'índex de Hurst del fBm, que descriu la intensitat de l'Efecte Josep.

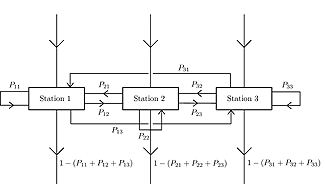
En el treball de recerca dut a terme, es considera un model de fluid no determinista a una xarxa composada per J estacions amb un únic servidor que processa fluid a taxa constant, sota disciplina FIFO (first-in-first-out), i un buffer infinit a cadascuna, amb  feedback (o retroalimentació, que vol dir que una proporció del fluid que surt d'una estació j se'n va seguidament a cada estació k per a ser re-processat, diguem Pjk, i la resta deixa la xarxa). La figura mostra el fluid entrant i sortint de la xarxa i entre estacions pel cas J=3. El procés d'arribades externes es suposa un procés acumulat agregat no determinista generat per un gran nombre de fonts On/Off amb cues pesades, similar al de Taqqu et al.

En aquest context, es prova que fent un canvi d'escala adequat, el procés de càrrega de treball immediat, que mesura la congestió i retràs a la xarxa, definit com la quantitat de temps requerit per cada servidor per a completar el processat de tot el fluid en cua (o essent processat) a cada instant, convergeix a un procés fBm J-dimensional, reflectit per tal de ser  positiu (ja que la càrrega de treball és positiva), sota tràfic intens. La condició de tràfic intens estableix que la càrrega total imposada en cada estació de servei tendeix a ser igual a la seva capacitat de processat  (és a dir, la intensitat de tràfic, definida com la taxa de fluid a través de les estacions dividit per la taxa de processat, tendeix a 1).

Aquest teorema és una generalització d'un resultat de Debicki i Mandjes (2004) per a models de fluid sobre xarxes amb una única estació, al context multi-estació i amb retroalimentació. 

L'interès de l'article és la seva contribució a la modelització estocàstica del tràfic sobre xarxes i l'estudi del procés fBm amb reflexió multi-dimensional en relació amb ella.