Two more dimensions to explain dark energy
Einstein introduced into his equations a cosmological constant in order to explain a static universe. Who would have thought that some years later this same constant would help to deduce another small detail: the acceleration of the expansion of the Universe? A team of UAB physicists has developed a physical model to conciliate the famous Constant in the Quantum Field Theory, connecting neutrino oscillations with dark energy.
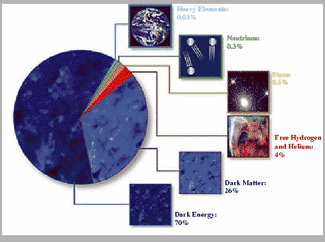
Einstein introduced the Cosmological Constant (CC) into his equations on General Relativity to describe a stationary Universe, but shortly after it was discovered that the Universe was in fact expanding. Einstein always regretted introducing this constant, but what is interesting is that this constant has been measured and its value is Λ~10-123 Mpl4 (with Mpl being the mass of Planck). And it is here, in the attempt to explain such a small number, where the fundamental problems of Cosmology begin, what is known as the Problem of the Cosmological Constant. Simultaneously the study of the speed of expansion of the Universe at cosmological distances using supernovas, as well as the analysis of the fluctuations of temperature of background radiation in the Universe, have provided surprising evidence that the expansion of the Universe is accelerating. Both pieces of evidence show that the density of the energy of the Universe has a new component called Dark Energy, which in fact is the dominant form since it constitutes 70% of the density of the energy in the Universe. This discovery has shed new light on the problem of CC given that in the context of a Quantum Theory of Fields this CC is interpreted as the density of the energy of vacuum with a value equivalent in that language of ρ~(10-3eV)4. The tremendously small value of this CC or density of the energy of vacuum does not coincide by many orders of magnitude with calculations made with the Quantum Theory of Fields.
The basic idea of the problem is the following: the density of the energy of vacuum at low energies may be written as the sum of its value calculated at the scale of microscopic theory plus the result of integrating the contributions of all the particles between the scale of fundamental theory and the scale of low energies. Calculating the contribution of these particles of mass m at the density of the energy of vacuum in 4 dimensions (3 space+1 time) we find that the result is of the order of m4, and that, for the simple electron is a terribly great contribution (5x105 eV)4. We need to find, then, a mechanism that will change the gravitational answer of vacuum to scales of the order of 10-3 eV and that is, precisely, what a model which incorporates extra dimensions (more than the normal 4 normal) combined with super symmetry (symmetry between bosons and fermions) achieves.
The model we propose, called MSLED or "Minimal Super symmetric Large Extra Dimensions", basically consists of a model of 6-dimensional super gravity where all the particles observed move in what we call a 3-brana (4-dimensional sub-space) immersed in an extra-dimensional world with two great extra-dimensions of the order of 10μm. The problem of CC then becomes a problem in 6 dimensions: now naturally the contribution of the particles at the density of the energy of vacuum is proportional to the scale of breakage of super symmetry in the extra-dimensions (msb~10-3 eV), which is related to the size of these dimensions. The substitution of the mass (m) of the particles by this small scale (msb) allows us to achieve a reproduction of the density of the energy of vacuum observed experimentally.
The observational implications of this model, which is very predictive, cover from cosmology, tests of gravity, and the physics of collisionators and neutrino physics. In this last field, the coincidence between the scale of difference of mass of neutrons observed and the density of Dark Energy suggests that we investigate a possible connexion between these quantities. Besides the specific characteristics of the MSLED model justify many of the ad hoc hypotheses of previous models: the fermionic fields in the extra dimensions are without mass due to super symmetry, the quantum corrections to the masses of the neutrinos are small due to a symmetry that is a natural extension of the leptonic number and, finally, surrounding conditions are automatically established by the extra-dimensional fermions which resolves serious problem in previous models of extra dimensions by neutrinos. Therefore, we have constructed a model, which apart from proposing a solution to the problem of CC gives rise to a good description of the experimental data of neutrino oscillation.
References
Article: J. Matias and C.P. Burgess, "MSLED, Neutrino oscillations and the Cosmological Constant", JHEP 0509 (2005) 052

